`core` ¶

`angle(ts, threshold=0.01, loss_func='re')` ¶

求时间序列ts拟合直线相对于x轴的夹角的余弦值

本函数可以用来判断时间序列的增长趋势。当angle处于[-1, 0]时，越靠近0，下降越快；当angle 处于[0, 1]时，越接近0，上升越快。

如果ts无法很好地拟合为直线，则返回[float, None]

Examples:

>>> ts = np.array([ i for i in range(5)])
>>> round(angle(ts)[1], 3) # degree: 45, rad: pi/2
0.707

>>> ts = np.array([ np.sqrt(3) / 3 * i for i in range(10)])
>>> round(angle(ts)[1],3) # degree: 30, rad: pi/6
0.866

>>> ts = np.array([ -np.sqrt(3) / 3 * i for i in range(7)])
>>> round(angle(ts)[1], 3) # degree: 150, rad: 5*pi/6
-0.866

Parameters:

Name	Type	Description	Default
`ts`			required

Returns:

Type	Description
`Tuple[float, float]`	返回 (error, consine(theta))，即拟合误差和夹角余弦值。

Source code in omicron/talib/core.py

def angle(ts, threshold=0.01, loss_func="re") -> Tuple[float, float]:
    """求时间序列`ts`拟合直线相对于`x`轴的夹角的余弦值

    本函数可以用来判断时间序列的增长趋势。当`angle`处于[-1, 0]时，越靠近0，下降越快；当`angle`
    处于[0, 1]时，越接近0，上升越快。

    如果`ts`无法很好地拟合为直线，则返回[float, None]

    Examples:

        >>> ts = np.array([ i for i in range(5)])
        >>> round(angle(ts)[1], 3) # degree: 45, rad: pi/2
        0.707

        >>> ts = np.array([ np.sqrt(3) / 3 * i for i in range(10)])
        >>> round(angle(ts)[1],3) # degree: 30, rad: pi/6
        0.866

        >>> ts = np.array([ -np.sqrt(3) / 3 * i for i in range(7)])
        >>> round(angle(ts)[1], 3) # degree: 150, rad: 5*pi/6
        -0.866

    Args:
        ts:

    Returns:
        返回 (error, consine(theta))，即拟合误差和夹角余弦值。

    """
    err, (a, b) = polyfit(ts, deg=1, loss_func=loss_func)
    if err > threshold:
        return (err, None)

    v = np.array([1, a + b])
    vx = np.array([1, 0])

    return err, copysign(np.dot(v, vx) / (norm(v) * norm(vx)), a)

`clustering(numbers, n)` ¶

将数组numbers划分为n个簇

返回值为一个List, 每一个元素为一个列表，分别为簇的起始点和长度。

Examples:

>>> numbers = np.array([1,1,1,2,4,6,8,7,4,5,6])
>>> clustering(numbers, 2)
[(0, 4), (4, 7)]

Returns:

Type	Description
`List[Tuple[int, int]]`	划分后的簇列表。

Source code in omicron/talib/core.py

def clustering(numbers: np.ndarray, n: int) -> List[Tuple[int, int]]:
    """将数组`numbers`划分为`n`个簇

    返回值为一个List, 每一个元素为一个列表，分别为簇的起始点和长度。

    Examples:
        >>> numbers = np.array([1,1,1,2,4,6,8,7,4,5,6])
        >>> clustering(numbers, 2)
        [(0, 4), (4, 7)]

    Returns:
        划分后的簇列表。
    """
    result = ckwrap.cksegs(numbers, n)

    clusters = []
    for pos, size in zip(result.centers, result.sizes):
        clusters.append((int(pos - size // 2 - 1), int(size)))

    return clusters

`exp_moving_average(values, window)` ¶

Numpy implementation of EMA

Source code in omicron/talib/core.py

def exp_moving_average(values, window):
    """Numpy implementation of EMA"""
    weights = np.exp(np.linspace(-1.0, 0.0, window))
    weights /= weights.sum()
    a = np.convolve(values, weights, mode="full")[: len(values)]
    a[:window] = a[window]

    return a

`mean_absolute_error(y, y_hat)` ¶

返回预测序列相对于真值序列的平均绝对值差

两个序列应该具有相同的长度。如果存在nan，则nan的值不计入平均值。

Examples:

>>> y = np.arange(5)
>>> y_hat = np.arange(5)
>>> y_hat[4] = 0
>>> mean_absolute_error(y, y)
0.0

>>> mean_absolute_error(y, y_hat)
0.8

Parameters:

Name	Type	Description	Default
`y`	`np.array`	真值序列	required
`y_hat`	`<built-in function array>`	比较序列	required

Returns:

Type	Description
`float`	平均绝对值差

Source code in omicron/talib/core.py

def mean_absolute_error(y: np.array, y_hat: np.array) -> float:
    """返回预测序列相对于真值序列的平均绝对值差

    两个序列应该具有相同的长度。如果存在nan，则nan的值不计入平均值。

    Examples:

        >>> y = np.arange(5)
        >>> y_hat = np.arange(5)
        >>> y_hat[4] = 0
        >>> mean_absolute_error(y, y)
        0.0

        >>> mean_absolute_error(y, y_hat)
        0.8

    Args:
        y (np.array): 真值序列
        y_hat: 比较序列

    Returns:
        float: 平均绝对值差
    """
    return nanmean(np.abs(y - y_hat))

`moving_average(ts, win, padding=True)` ¶

生成ts序列的移动平均值

Examples:

>>> ts = np.arange(7)
>>> moving_average(ts, 5)
array([nan, nan, nan, nan,  2.,  3.,  4.])

Parameters:

Name	Type	Description	Default
`ts`	`Sequence`	the input array	required
`win`	`int`	the window size	required
`padding`		if True, then the return will be equal length as input, padding with np.NaN at the beginning	`True`

Returns:

Type	Description
`ndarray`	The moving mean of the input array along the specified axis. The output has the same shape as the input.

Source code in omicron/talib/core.py

def moving_average(ts: Sequence, win: int, padding=True) -> np.ndarray:
    """生成ts序列的移动平均值

    Examples:

        >>> ts = np.arange(7)
        >>> moving_average(ts, 5)
        array([nan, nan, nan, nan,  2.,  3.,  4.])

    Args:
        ts (Sequence): the input array
        win (int): the window size
        padding: if True, then the return will be equal length as input, padding with np.NaN at the beginning

    Returns:
        The moving mean of the input array along the specified axis. The output has the same shape as the input.
    """
    ma = move_mean(ts, win)
    if padding:
        return ma
    else:
        return ma[win - 1 :]

`normalize(X, scaler='maxabs')` ¶

对数据进行规范化处理。

如果scaler为maxabs，则X的各元素被压缩到[-1,1]之间如果scaler为unit_vector，则将X的各元素压缩到单位范数如果scaler为minmax,则X的各元素被压缩到[0,1]之间如果scaler为standard,则X的各元素被压缩到单位方差之间，且均值为零。

参考 sklearn

Examples:

>>> X = [[ 1., -1.,  2.],
... [ 2.,  0.,  0.],
... [ 0.,  1., -1.]]

>>> expected = [[ 0.4082, -0.4082,  0.8165],
... [ 1.,  0.,  0.],
... [ 0.,  0.7071, -0.7071]]

>>> X_hat = normalize(X, scaler='unit_vector')
>>> np.testing.assert_array_almost_equal(expected, X_hat, decimal=4)

>>> expected = [[0.5, -1., 1.],
... [1., 0., 0.],
... [0., 1., -0.5]]

>>> X_hat = normalize(X, scaler='maxabs')
>>> np.testing.assert_array_almost_equal(expected, X_hat, decimal = 2)

>>> expected = [[0.5       , 0.        , 1.        ],
... [1.        , 0.5       , 0.33333333],
... [0.        , 1.        , 0.        ]]
>>> X_hat = normalize(X, scaler='minmax')
>>> np.testing.assert_array_almost_equal(expected, X_hat, decimal= 3)

>>> X = [[0, 0],
... [0, 0],
... [1, 1],
... [1, 1]]
>>> expected = [[-1., -1.],
... [-1., -1.],
... [ 1., 1.],
... [ 1.,  1.]]
>>> X_hat = normalize(X, scaler='standard')
>>> np.testing.assert_array_almost_equal(expected, X_hat, decimal = 3)

Parameters:

Name	Type	Description	Default
`X`	`2D array`		required
`scaler`	`str`	[description]. Defaults to 'maxabs_scale'.	`'maxabs'`

Source code in omicron/talib/core.py

def normalize(X, scaler="maxabs"):
    """对数据进行规范化处理。

    如果scaler为maxabs，则X的各元素被压缩到[-1,1]之间
    如果scaler为unit_vector，则将X的各元素压缩到单位范数
    如果scaler为minmax,则X的各元素被压缩到[0,1]之间
    如果scaler为standard,则X的各元素被压缩到单位方差之间，且均值为零。

    参考 [sklearn]

    [sklearn]: https://scikit-learn.org/stable/auto_examples/preprocessing/plot_all_scaling.html#results

    Examples:

        >>> X = [[ 1., -1.,  2.],
        ... [ 2.,  0.,  0.],
        ... [ 0.,  1., -1.]]

        >>> expected = [[ 0.4082, -0.4082,  0.8165],
        ... [ 1.,  0.,  0.],
        ... [ 0.,  0.7071, -0.7071]]

        >>> X_hat = normalize(X, scaler='unit_vector')
        >>> np.testing.assert_array_almost_equal(expected, X_hat, decimal=4)

        >>> expected = [[0.5, -1., 1.],
        ... [1., 0., 0.],
        ... [0., 1., -0.5]]

        >>> X_hat = normalize(X, scaler='maxabs')
        >>> np.testing.assert_array_almost_equal(expected, X_hat, decimal = 2)

        >>> expected = [[0.5       , 0.        , 1.        ],
        ... [1.        , 0.5       , 0.33333333],
        ... [0.        , 1.        , 0.        ]]
        >>> X_hat = normalize(X, scaler='minmax')
        >>> np.testing.assert_array_almost_equal(expected, X_hat, decimal= 3)

        >>> X = [[0, 0],
        ... [0, 0],
        ... [1, 1],
        ... [1, 1]]
        >>> expected = [[-1., -1.],
        ... [-1., -1.],
        ... [ 1., 1.],
        ... [ 1.,  1.]]
        >>> X_hat = normalize(X, scaler='standard')
        >>> np.testing.assert_array_almost_equal(expected, X_hat, decimal = 3)

    Args:
        X (2D array):
        scaler (str, optional): [description]. Defaults to 'maxabs_scale'.
    """
    if scaler == "maxabs":
        return MaxAbsScaler().fit_transform(X)
    elif scaler == "unit_vector":
        return sklearn.preprocessing.normalize(X, norm="l2")
    elif scaler == "minmax":
        return minmax_scale(X)
    elif scaler == "standard":
        return StandardScaler().fit_transform(X)

`pct_error(y, y_hat)` ¶

相对于序列算术均值的误差值

Examples:

>>> y = np.arange(5)
>>> y_hat = np.arange(5)
>>> y_hat[4] = 0
>>> pct_error(y, y_hat)
0.4

Parameters:

Name	Type	Description	Default
`y`	`np.array`	[description]	required
`y_hat`	`np.array`	[description]	required

Returns:

Type	Description
`float`	[description]

Source code in omicron/talib/core.py

def pct_error(y: np.array, y_hat: np.array) -> float:
    """相对于序列算术均值的误差值

    Examples:
        >>> y = np.arange(5)
        >>> y_hat = np.arange(5)
        >>> y_hat[4] = 0
        >>> pct_error(y, y_hat)
        0.4

    Args:
        y (np.array): [description]
        y_hat (np.array): [description]

    Returns:
        float: [description]
    """
    mae = mean_absolute_error(y, y_hat)
    return mae / nanmean(np.abs(y))

`polyfit(ts, deg=2, loss_func='re')` ¶

对给定的时间序列进行直线/二次曲线拟合。

二次曲线可以拟合到反生反转的行情，如圆弧底、圆弧顶；也可以拟合到上述趋势中的单边走势，即其中一段曲线。对于如长期均线，在一段时间内走势可能呈现为一条直线，故也可用此函数进行直线拟合。

为便于在不同品种、不同的时间之间对误差、系数进行比较，请事先对ts进行归一化。如果遇到无法拟合的情况（异常），将返回一个非常大的误差，并将其它项置为np.nan

Examples:

>>> ts = [i for i in range(5)]
>>> err, (a, b) = polyfit(ts, deg=1)
>>> print(round(err, 3), round(a, 1))
0.0 1.0

Parameters:

Name	Type	Description	Default
`ts`	`Sequence`	待拟合的时间序列	required
`deg`	`int`	如果要进行直线拟合，取1；二次曲线拟合取2. Defaults to 2	`2`
`loss_func`	`str`	误差计算方法，取值为`mae`, `rmse`,`mse` 或`re`。Defaults to `re` (relative_error)	`'re'`

Returns:

Type	Description
`[Tuple]`	如果为直线拟合，返回误差，(a,b)(一次项系数和常数)。如果为二次曲线拟合，返回误差, (a,b,c)(二次项、一次项和常量）, (vert_x, vert_y)(顶点处的index，顶点值)

Source code in omicron/talib/core.py

def polyfit(ts: Sequence, deg: int = 2, loss_func="re") -> Tuple:
    """对给定的时间序列进行直线/二次曲线拟合。

    二次曲线可以拟合到反生反转的行情，如圆弧底、圆弧顶；也可以拟合到上述趋势中的单边走势，即其中一段曲线。对于如长期均线，在一段时间内走势可能呈现为一条直线，故也可用此函数进行直线拟合。

    为便于在不同品种、不同的时间之间对误差、系数进行比较，请事先对ts进行归一化。
    如果遇到无法拟合的情况（异常），将返回一个非常大的误差，并将其它项置为np.nan

    Examples:
        >>> ts = [i for i in range(5)]
        >>> err, (a, b) = polyfit(ts, deg=1)
        >>> print(round(err, 3), round(a, 1))
        0.0 1.0

    Args:
        ts (Sequence): 待拟合的时间序列
        deg (int): 如果要进行直线拟合，取1；二次曲线拟合取2. Defaults to 2
        loss_func (str): 误差计算方法，取值为`mae`, `rmse`,`mse` 或`re`。Defaults to `re` (relative_error)
    Returns:
        [Tuple]: 如果为直线拟合，返回误差，(a,b)(一次项系数和常数)。如果为二次曲线拟合，返回
        误差, (a,b,c)(二次项、一次项和常量）, (vert_x, vert_y)(顶点处的index，顶点值)
    """
    if deg not in (1, 2):
        raise ValueError("deg must be 1 or 2")

    try:
        if any(np.isnan(ts)):
            raise ValueError("ts contains nan")

        x = np.array(list(range(len(ts))))

        z = np.polyfit(x, ts, deg=deg)

        p = np.poly1d(z)
        ts_hat = np.array([p(xi) for xi in x])

        if loss_func == "mse":
            error = np.mean(np.square(ts - ts_hat))
        elif loss_func == "rmse":
            error = np.sqrt(np.mean(np.square(ts - ts_hat)))
        elif loss_func == "mae":
            error = mean_absolute_error(ts, ts_hat)
        else:  # defaults to relative error
            error = pct_error(ts, ts_hat)

        if deg == 2:
            a, b, c = z[0], z[1], z[2]
            axis_x = -b / (2 * a)
            if a != 0:
                axis_y = (4 * a * c - b * b) / (4 * a)
            else:
                axis_y = None
            return error, z, (axis_x, axis_y)
        elif deg == 1:
            return error, z
    except Exception:
        error = 1e9
        if deg == 1:
            return error, (np.nan, np.nan)
        else:
            return error, (np.nan, np.nan, np.nan), (np.nan, np.nan)

`slope(ts, loss_func='re')` ¶

求ts表示的直线（如果能拟合成直线的话）的斜率

Parameters:

Name	Type	Description	Default
`ts`	`np.array`	[description]	required
`loss_func`	`str`	[description]. Defaults to 're'.	`'re'`

Source code in omicron/talib/core.py

def slope(ts: np.array, loss_func="re"):
    """求ts表示的直线（如果能拟合成直线的话）的斜率

    Args:
        ts (np.array): [description]
        loss_func (str, optional): [description]. Defaults to 're'.
    """
    err, (a, b) = polyfit(ts, deg=1, loss_func=loss_func)

    return err, a

`smooth(ts, win, poly_order=1, mode='interp')` ¶

平滑序列ts，使用窗口大小为win的平滑模型，默认使用线性模型

提供本函数主要基于这样的考虑： omicron的使用者可能并不熟悉信号处理的概念，这里相当于提供了相关功能的一个入口。

Parameters:

Name	Type	Description	Default
`ts`	`np.array`	[description]	required
`win`	`int`	[description]	required
`poly_order`	`int`	[description]. Defaults to 1.	`1`

Source code in omicron/talib/core.py

def smooth(ts: np.array, win: int, poly_order=1, mode="interp"):
    """平滑序列ts，使用窗口大小为win的平滑模型，默认使用线性模型

    提供本函数主要基于这样的考虑： omicron的使用者可能并不熟悉信号处理的概念，这里相当于提供了相关功能的一个入口。

    Args:
        ts (np.array): [description]
        win (int): [description]
        poly_order (int, optional): [description]. Defaults to 1.
    """
    return savgol_filter(ts, win, poly_order, mode=mode)

`weighted_moving_average(ts, win)` ¶

计算加权移动平均

Parameters:

Name	Type	Description	Default
`ts`	`np.array`	[description]	required
`win`	`int`	[description]	required

Returns:

Type	Description
`np.array`	[description]

Source code in omicron/talib/core.py

def weighted_moving_average(ts: np.array, win: int) -> np.array:
    """计算加权移动平均

    Args:
        ts (np.array): [description]
        win (int): [description]

    Returns:
        np.array: [description]
    """
    w = [2 * (i + 1) / (win * (win + 1)) for i in range(win)]

    return np.convolve(ts, w, "valid")

`morph` ¶

形态检测相关方法

`BreakoutFlag (IntEnum)` ¶

An enumeration.

Source code in omicron/talib/morph.py

class BreakoutFlag(IntEnum):
    UP = 1
    DOWN = -1
    NONE = 0

`CrossFlag (IntEnum)` ¶

An enumeration.

Source code in omicron/talib/morph.py

class CrossFlag(IntEnum):
    UPCROSS = 1
    DOWNCROSS = -1
    NONE = 0

`breakout(ts, upthres=0.01, downthres=-0.01, confirm=1)` ¶

检测时间序列是否突破了压力线（整理线）

Parameters:

Name	Type	Description	Default
`ts`	`np.ndarray`	时间序列	required
`upthres`	`float`	请参考peaks_and_valleys	`0.01`
`downthres`	`float`	请参考peaks_and_valleys	`-0.01`
`confirm`	`int`	经过多少个bars后，才确认突破。默认为1	`1`

Returns:

Type	Description
`BreakoutFlag`	如果上向突破压力线，返回1，如果向下突破压力线，返回-1，否则返回0

Source code in omicron/talib/morph.py

def breakout(
    ts: np.ndarray, upthres: float = 0.01, downthres: float = -0.01, confirm: int = 1
) -> BreakoutFlag:
    """检测时间序列是否突破了压力线（整理线）

    Args:
        ts (np.ndarray): 时间序列
        upthres (float, optional): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]
        downthres (float, optional): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]
        confirm (int, optional): 经过多少个bars后，才确认突破。默认为1

    Returns:
        如果上向突破压力线，返回1，如果向下突破压力线，返回-1，否则返回0
    """
    support, resist, _ = support_resist_lines(ts[:-confirm], upthres, downthres)

    x0 = len(ts) - confirm - 1
    x = list(range(len(ts) - confirm, len(ts)))

    if resist is not None:
        if np.all(ts[x] > resist(x)) and ts[x0] <= resist(x0):
            return BreakoutFlag.UP

    if support is not None:
        if np.all(ts[x] < support(x)) and ts[x0] >= support(x0):
            return BreakoutFlag.DOWN

    return BreakoutFlag.NONE

`cross(f, g)` ¶

判断序列f是否与g相交。如果两个序列有且仅有一个交点，则返回1表明f上交g；-1表明f下交g

本方法可用以判断两条均线是否相交。

Returns:

Type	Description
`CrossFlag`	(flag, index), 其中flag取值为： 0 无效 -1 f向下交叉g 1 f向上交叉g

Source code in omicron/talib/morph.py

def cross(f: np.ndarray, g: np.ndarray) -> CrossFlag:
    """判断序列f是否与g相交。如果两个序列有且仅有一个交点，则返回1表明f上交g；-1表明f下交g

    本方法可用以判断两条均线是否相交。

    returns:
        (flag, index), 其中flag取值为：
        0 无效
        -1 f向下交叉g
        1 f向上交叉g
    """
    indices = np.argwhere(np.diff(np.sign(f - g))).flatten()

    if len(indices) == 0:
        return CrossFlag.NONE, 0

    # 如果存在一个或者多个交点，取最后一个
    idx = indices[-1]

    if f[idx] < g[idx]:
        return CrossFlag.UPCROSS, idx
    elif f[idx] > g[idx]:
        return CrossFlag.DOWNCROSS, idx
    else:
        return CrossFlag(np.sign(g[idx - 1] - f[idx - 1])), idx

`energy_hump(bars, thresh=2)` ¶

检测bars中是否存在两波以上量能剧烈增加的情形（能量驼峰），返回最后一波距现在的位置及区间长度。

注意如果最后一个能量驼峰距现在过远（比如超过10个bar),可能意味着资金已经逃离，能量已经耗尽。

Parameters:

Name	Type	Description	Default
`bars`	`[('frame', '<M8[s]'), ('open', '<f4'), ('high', '<f4'), ('low', '<f4'), ('close', '<f4'), ('volume', '<f8'), ('amount', '<f8'), ('factor', '<f4')]`	行情数据	required
`thresh`		最后一波量必须大于20天均量的倍数。	`2`

Returns:

Type	Description
`Optional[Tuple[int, int]]`	如果不存在能量驼峰的情形，则返回None，否则返回最后一个驼峰离现在的距离及区间长度。

Source code in omicron/talib/morph.py

def energy_hump(bars: bars_dtype, thresh=2) -> Optional[Tuple[int, int]]:
    """检测`bars`中是否存在两波以上量能剧烈增加的情形（能量驼峰），返回最后一波距现在的位置及区间长度。

    注意如果最后一个能量驼峰距现在过远（比如超过10个bar),可能意味着资金已经逃离，能量已经耗尽。

    Args:
        bars: 行情数据
        thresh: 最后一波量必须大于20天均量的倍数。
    Returns:
        如果不存在能量驼峰的情形，则返回None，否则返回最后一个驼峰离现在的距离及区间长度。
    """
    vol = bars["volume"]

    std = np.std(vol[1:] / vol[:-1])
    pvs = peak_valley_pivots(vol, std, 0)

    frames = bars["frame"]

    pvs[0] = 0
    pvs[-1] = -1
    peaks = np.argwhere(pvs == 1)

    mn = np.mean(vol[peaks])

    # 顶点不能缩量到尖峰均值以下
    real_peaks = np.intersect1d(np.argwhere(vol > mn), peaks)

    if len(real_peaks) < 2:
        return None

    logger.debug("found %s peaks at %s", len(real_peaks), frames[real_peaks])
    lp = real_peaks[-1]
    ma = moving_average(vol, 20)[lp]
    if vol[lp] < ma * thresh:
        logger.debug(
            "vol of last peak[%s] is less than mean_vol(20) * thresh[%s]",
            vol[lp],
            ma * thresh,
        )
        return None

    return len(bars) - real_peaks[-1], real_peaks[-1] - real_peaks[0]

`inverse_vcross(f, g)` ¶

判断序列f是否与序列g存在^型相交。即存在两个交点，第一个交点为向上相交，第二个交点为向下相交。可用于判断见顶特征等场合。

Parameters:

Name	Type	Description	Default
`f`	`np.array`	[description]	required
`g`	`np.array`	[description]	required

Returns:

Type	Description
`Tuple`	[description]

Source code in omicron/talib/morph.py

def inverse_vcross(f: np.array, g: np.array) -> Tuple:
    """判断序列f是否与序列g存在^型相交。即存在两个交点，第一个交点为向上相交，第二个交点为向下
    相交。可用于判断见顶特征等场合。

    Args:
        f (np.array): [description]
        g (np.array): [description]

    Returns:
        Tuple: [description]
    """
    indices = np.argwhere(np.diff(np.sign(f - g))).flatten()
    if len(indices) == 2:
        idx0, idx1 = indices
        if f[idx0] < g[idx0] and f[idx1] > g[idx1]:
            return True, (idx0, idx1)

    return False, (None, None)

`peaks_and_valleys(ts, up_thresh=None, down_thresh=None)` ¶

寻找ts中的波峰和波谷，返回数组指示在该位置上是否为波峰或波谷。如果为1，则为波峰；如果为-1，则为波谷。

本函数直接使用了zigzag中的peak_valley_pivots. 有很多方法可以实现本功能，比如scipy.signals.find_peaks_cwt, peak_valley_pivots等。本函数更适合金融时间序列，并且使用了cython加速。

Parameters:

Name	Type	Description	Default
`ts`	`np.ndarray`	时间序列	required
`up_thresh`	`float`	波峰的阈值，如果为None,则使用ts变化率的二倍标准差	`None`
`down_thresh`	`float`	波谷的阈值，如果为None,则使用ts变化率的二倍标准差乘以-1	`None`

Returns:

Type	Description
`np.ndarray`	返回数组指示在该位置上是否为波峰或波谷。

Source code in omicron/talib/morph.py

def peaks_and_valleys(
    ts: np.ndarray,
    up_thresh: Optional[float] = None,
    down_thresh: Optional[float] = None,
) -> np.ndarray:
    """寻找ts中的波峰和波谷，返回数组指示在该位置上是否为波峰或波谷。如果为1，则为波峰；如果为-1，则为波谷。

    本函数直接使用了zigzag中的peak_valley_pivots. 有很多方法可以实现本功能，比如scipy.signals.find_peaks_cwt, peak_valley_pivots等。本函数更适合金融时间序列，并且使用了cython加速。

    Args:
        ts (np.ndarray): 时间序列
        up_thresh (float): 波峰的阈值，如果为None,则使用ts变化率的二倍标准差
        down_thresh (float): 波谷的阈值，如果为None,则使用ts变化率的二倍标准差乘以-1

    Returns:
        np.ndarray: 返回数组指示在该位置上是否为波峰或波谷。
    """
    if ts.dtype != np.float64:
        ts = ts.astype(np.float64)

    if any([up_thresh is None, down_thresh is None]):
        change_rate = ts[1:] / ts[:-1] - 1
        std = np.std(change_rate)
        up_thresh = up_thresh or 2 * std
        down_thresh = down_thresh or -2 * std

    return peak_valley_pivots(ts, up_thresh, down_thresh)

`plateaus(numbers, min_size, fall_in_range_ratio=0.97)` ¶

统计数组numbers中的可能存在的平台整理。

如果一个数组中存在着子数组，使得其元素与均值的距离落在三个标准差以内的比例超过fall_in_range_ratio的，则认为该子数组满足平台整理。

Parameters:

Name	Type	Description	Default
`numbers`	`ndarray`	输入数组	required
`min_size`	`int`	平台的最小长度	required
`fall_in_range_ratio`	`float`	超过`fall_in_range_ratio`比例的元素落在均值的三个标准差以内，就认为该子数组构成一个平台	`0.97`

Returns:

Type	Description
`List[Tuple]`	平台的起始位置和长度的数组

Source code in omicron/talib/morph.py

def plateaus(
    numbers: np.ndarray, min_size: int, fall_in_range_ratio: float = 0.97
) -> List[Tuple]:
    """统计数组`numbers`中的可能存在的平台整理。

    如果一个数组中存在着子数组，使得其元素与均值的距离落在三个标准差以内的比例超过`fall_in_range_ratio`的，则认为该子数组满足平台整理。

    Args:
        numbers: 输入数组
        min_size: 平台的最小长度
        fall_in_range_ratio: 超过`fall_in_range_ratio`比例的元素落在均值的三个标准差以内，就认为该子数组构成一个平台

    Returns:
        平台的起始位置和长度的数组
    """
    if numbers.size <= min_size:
        n = 1
    else:
        n = numbers.size // min_size

    clusters = clustering(numbers, n)

    plats = []
    for (start, length) in clusters:
        if length < min_size:
            continue

        y = numbers[start : start + length]
        mean = np.mean(y)
        std = np.std(y)

        inrange = len(y[np.abs(y - mean) < 3 * std])
        ratio = inrange / length

        if ratio >= fall_in_range_ratio:
            plats.append((start, length))

    return plats

`rsi_bottom_distance(close, thresh=None)` ¶

根据给定的收盘价，计算最后一个数据到上一个发出rsi低水平的距离，如果从上一个最低点rsi到最后一个数据并未发出低水平信号，返回最后一个数据到上一个发出最低点rsi的距离。

其中close的长度一般不小于60。返回值为距离整数，不满足条件则返回None。

Parameters:

Name	Type	Description	Default
`close`	`np.array`	具有时间序列的收盘价	required
`thresh`	`Tuple[float, float])`	None适用所有股票，不必更改，也可自行设置。	`None`

Returns:

Type	Description
`int`	返回最后一个数据到上一个发出rsi低水平的距离。如果从上一个最低点rsi到最后一个数据并未发出低水平信号，返回最后一个数据到上一个发出最低点rsi的距离。除此之外，返回None。

Source code in omicron/talib/morph.py

def rsi_bottom_distance(close: np.array, thresh: Tuple[float, float] = None) -> int:
    """根据给定的收盘价，计算最后一个数据到上一个发出rsi低水平的距离，
    如果从上一个最低点rsi到最后一个数据并未发出低水平信号，
    返回最后一个数据到上一个发出最低点rsi的距离。

    其中close的长度一般不小于60。
    返回值为距离整数，不满足条件则返回None。

    Args:
        close (np.array): 具有时间序列的收盘价
        thresh (Tuple[float, float]) : None适用所有股票，不必更改，也可自行设置。

    Returns:
        返回最后一个数据到上一个发出rsi低水平的距离。
        如果从上一个最低点rsi到最后一个数据并未发出低水平信号，
        返回最后一个数据到上一个发出最低点rsi的距离。
        除此之外，返回None。"""

    assert len(close) >= 60, "must provide an array with at least 60 length!"

    if close.dtype != np.float64:
        close = close.astype(np.float64)

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    rsi = ta.RSI(close, 6)

    watermarks = rsi_watermarks(close, thresh)
    if watermarks is not None:
        low_watermark, _, _ = watermarks
        pivots = peak_valley_pivots(close, thresh[0], thresh[1])
        pivots[0], pivots[-1] = 0, 0

        # 谷值RSI<30
        valley_rsi_index = np.where((rsi < 30) & (pivots == -1))[0]

        # RSI低水平的最大值：低水平*1.01
        low_rsi_index = np.where(rsi <= low_watermark * 1.01)[0]

        if len(valley_rsi_index) > 0:
            distance = len(rsi) - 1 - valley_rsi_index[-1]
            if len(low_rsi_index) > 0:
                if low_rsi_index[-1] >= valley_rsi_index[-1]:
                    distance = len(rsi) - 1 - low_rsi_index[-1]
            return distance

`rsi_bottom_divergent(close, thresh=None, rsi_limit=30)` ¶

寻找最近满足条件的rsi底背离。

返回最后一个数据到最近底背离发生点的距离；没有满足条件的底背离，返回None。

Parameters:

Name	Type	Description	Default
`close`	`np.array`	时间序列收盘价	required
`thresh`	`Tuple[float, float]`	请参考peaks_and_valleys	`None`
`rsi_limit`	`float`	RSI发生底背离时的阈值, 默认值30（20效果更佳，但是检测出来数量太少），即只过滤RSI6<30的局部最低收盘价。	`30`

Returns:

Type	Description
`int`	返回int类型的整数，表示最后一个数据到最近底背离发生点的距离；没有满足条件的底背离，返回None。

Source code in omicron/talib/morph.py

def rsi_bottom_divergent(
    close: np.array, thresh: Tuple[float, float] = None, rsi_limit: float = 30
) -> int:
    """寻找最近满足条件的rsi底背离。

    返回最后一个数据到最近底背离发生点的距离；没有满足条件的底背离，返回None。

    Args:
        close (np.array): 时间序列收盘价
        thresh (Tuple[float, float]): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]
        rsi_limit (float, optional): RSI发生底背离时的阈值, 默认值30（20效果更佳，但是检测出来数量太少），即只过滤RSI6<30的局部最低收盘价。

    Returns:
        返回int类型的整数，表示最后一个数据到最近底背离发生点的距离；没有满足条件的底背离，返回None。
    """
    assert len(close) >= 60, "must provide an array with at least 60 length!"
    if close.dtype != np.float64:
        close = close.astype(np.float64)
    rsi = ta.RSI(close, 6)

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    pivots = peak_valley_pivots(close, thresh[0], thresh[1])
    pivots[0], pivots[-1] = 0, 0

    length = len(close)
    valley_index = np.where((pivots == -1) & (rsi <= rsi_limit))[0]

    if len(valley_index) >= 2:
        if (close[valley_index[-1]] < close[valley_index[-2]]) and (
            rsi[valley_index[-1]] > rsi[valley_index[-2]]
        ):
            bottom_dev_distance = length - 1 - valley_index[-1]

            return bottom_dev_distance

`rsi_predict_price(close, thresh=None)` ¶

给定一段行情，根据最近的两个RSI的极小值和极大值预测下一个周期可能达到的最低价格和最高价格。

其原理是，以预测最近的两个最高价和最低价，求出其相对应的RSI值，求出最高价和最低价RSI的均值，若只有一个则取最近的一个。再由RSI公式，反推价格。此时返回值为(None, float)，即只有最高价，没有最低价。反之亦然。

Parameters:

Name	Type	Description	Default
`close`	`np.ndarray`	具有时间序列的收盘价	required
`thresh`	`Tuple[float, float])`	请参考peaks_and_valleys	`None`

Returns:

Type	Description
`Tuple[float, float]`	返回数组[predicted_low_price, predicted_high_price], 数组第一个值为利用达到之前最低收盘价的RSI预测的最低价。第二个值为利用达到之前最高收盘价的RSI预测的最高价。

Source code in omicron/talib/morph.py

def rsi_predict_price(
    close: np.ndarray, thresh: Tuple[float, float] = None
) -> Tuple[float, float]:
    """给定一段行情，根据最近的两个RSI的极小值和极大值预测下一个周期可能达到的最低价格和最高价格。

    其原理是，以预测最近的两个最高价和最低价，求出其相对应的RSI值，求出最高价和最低价RSI的均值，
    若只有一个则取最近的一个。再由RSI公式，反推价格。此时返回值为(None, float)，即只有最高价，没有最低价。反之亦然。

    Args:
        close (np.ndarray): 具有时间序列的收盘价
        thresh (Tuple[float, float]) : 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]

    Returns:
        返回数组[predicted_low_price, predicted_high_price], 数组第一个值为利用达到之前最低收盘价的RSI预测的最低价。
        第二个值为利用达到之前最高收盘价的RSI预测的最高价。
    """
    assert len(close) >= 60, "must provide an array with at least 60 length!"

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    if close.dtype != np.float64:
        close = close.astype(np.float64)

    valley_rsi, peak_rsi, _ = rsi_watermarks(close, thresh=thresh)
    pivot = peak_valley_pivots(close, thresh[0], thresh[1])
    pivot[0], pivot[-1] = 0, 0  # 掐头去尾

    price_change = pd.Series(close).diff(1).values
    ave_price_change = (abs(price_change)[-6:].mean()) * 5
    ave_price_raise = (np.maximum(price_change, 0)[-6:].mean()) * 5

    if valley_rsi is not None:
        predicted_low_change = (ave_price_change) - ave_price_raise / (
            0.01 * valley_rsi
        )
        if predicted_low_change > 0:
            predicted_low_change = 0
        predicted_low_price = close[-1] + predicted_low_change
    else:
        predicted_low_price = None

    if peak_rsi is not None:
        predicted_high_change = (ave_price_raise - ave_price_change) / (
            0.01 * peak_rsi - 1
        ) - ave_price_change
        if predicted_high_change < 0:
            predicted_high_change = 0
        predicted_high_price = close[-1] + predicted_high_change
    else:
        predicted_high_price = None

    return predicted_low_price, predicted_high_price

`rsi_top_distance(close, thresh=None)` ¶

根据给定的收盘价，计算最后一个数据到上一个发出rsi高水平的距离，如果从上一个最高点rsi到最后一个数据并未发出高水平信号，返回最后一个数据到上一个发出最高点rsi的距离。

其中close的长度一般不小于60。返回值为距离整数，不满足条件则返回None。

Parameters:

Name	Type	Description	Default
`close`	`np.array`	具有时间序列的收盘价	required
`thresh`	`Tuple[float, float])`	None适用所有股票，不必更改，也可自行设置。	`None`

Returns:

Type	Description
`int`	返回最后一个数据到上一个发出rsi高水平的距离。如果从上一个最高点rsi到最后一个数据并未发出高水平信号，返回最后一个数据到上一个发出最高点rsi的距离。除此之外，返回None。

Source code in omicron/talib/morph.py

def rsi_top_distance(close: np.array, thresh: Tuple[float, float] = None) -> int:
    """根据给定的收盘价，计算最后一个数据到上一个发出rsi高水平的距离，
    如果从上一个最高点rsi到最后一个数据并未发出高水平信号，
    返回最后一个数据到上一个发出最高点rsi的距离。

    其中close的长度一般不小于60。
    返回值为距离整数，不满足条件则返回None。

    Args:
        close (np.array): 具有时间序列的收盘价
        thresh (Tuple[float, float]) : None适用所有股票，不必更改，也可自行设置。

    Returns:
        返回最后一个数据到上一个发出rsi高水平的距离。
        如果从上一个最高点rsi到最后一个数据并未发出高水平信号，
        返回最后一个数据到上一个发出最高点rsi的距离。
        除此之外，返回None。"""

    assert len(close) >= 60, "must provide an array with at least 60 length!"

    if close.dtype != np.float64:
        close = close.astype(np.float64)

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    rsi = ta.RSI(close, 6)

    watermarks = rsi_watermarks(close, thresh)
    if watermarks is not None:
        _, high_watermark, _ = watermarks
        pivots = peak_valley_pivots(close, thresh[0], thresh[1])
        pivots[0], pivots[-1] = 0, 0

        # 峰值RSI>70
        peak_rsi_index = np.where((rsi > 70) & (pivots == 1))[0]

        # RSI高水平的最小值：高水平*0.99
        high_rsi_index = np.where(rsi >= high_watermark * 0.99)[0]

        if len(peak_rsi_index) > 0:
            distance = len(rsi) - 1 - peak_rsi_index[-1]
            if len(high_rsi_index) > 0:
                if high_rsi_index[-1] >= peak_rsi_index[-1]:
                    distance = len(rsi) - 1 - high_rsi_index[-1]
            return distance

`rsi_top_divergent(close, thresh=None, rsi_limit=70)` ¶

寻找最近满足条件的rsi顶背离。

返回最后一个数据到最近顶背离发生点的距离；没有满足条件的顶背离，返回None。

Parameters:

Name	Type	Description	Default
`close`	`np.array`	时间序列收盘价	required
`thresh`	`Tuple[float, float]`	请参考peaks_and_valleys	`None`
`rsi_limit`	`float`	RSI发生顶背离时的阈值, 默认值70（80效果更佳，但是检测出来数量太少），即只过滤RSI6>70的局部最高收盘价。	`70`

Returns:

Type	Description
`Tuple[int, int]`	返回int类型的整数，表示最后一个数据到最近顶背离发生点的距离；没有满足条件的顶背离，返回None。

Source code in omicron/talib/morph.py

def rsi_top_divergent(
    close: np.array, thresh: Tuple[float, float] = None, rsi_limit: float = 70
) -> Tuple[int, int]:
    """寻找最近满足条件的rsi顶背离。

    返回最后一个数据到最近顶背离发生点的距离；没有满足条件的顶背离，返回None。

    Args:
        close (np.array): 时间序列收盘价
        thresh (Tuple[float, float]): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]
        rsi_limit (float, optional): RSI发生顶背离时的阈值, 默认值70（80效果更佳，但是检测出来数量太少），即只过滤RSI6>70的局部最高收盘价。

    Returns:
        返回int类型的整数，表示最后一个数据到最近顶背离发生点的距离；没有满足条件的顶背离，返回None。
    """
    assert len(close) >= 60, "must provide an array with at least 60 length!"
    if close.dtype != np.float64:
        close = close.astype(np.float64)
    rsi = ta.RSI(close, 6)

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    pivots = peak_valley_pivots(close, thresh[0], thresh[1])
    pivots[0], pivots[-1] = 0, 0

    length = len(close)
    peak_index = np.where((pivots == 1) & (rsi >= rsi_limit))[0]

    if len(peak_index) >= 2:
        if (close[peak_index[-1]] > close[peak_index[-2]]) and (
            rsi[peak_index[-1]] < rsi[peak_index[-2]]
        ):
            top_dev_distance = length - 1 - peak_index[-1]

            return top_dev_distance

`rsi_watermarks(close, thresh=None)` ¶

给定一段行情数据和用以检测顶和底的阈值，返回该段行情中，谷和峰处RSI均值，最后一个RSI6值。

其中close的长度一般不小于60，不大于120。返回值中，一个为low_wartermark（谷底处RSI值），一个为high_wartermark（高峰处RSI值)，一个为RSI6的最后一个值，用以对比前两个警戒值。

Parameters:

Name	Type	Description	Default
`close`	`np.array`	具有时间序列的收盘价	required
`thresh`	`Tuple[float, float])`	None适用所有股票，不必更改，也可自行设置。	`None`

Returns:

Type	Description
`Tuple[float, float, float]`	返回数组[low_watermark, high_watermark， rsi[-1]], 第一个为最近两个最低收盘价的RSI均值，第二个为最近两个最高收盘价的RSI均值。若传入收盘价只有一个最值，只返回一个。没有最值，则返回None, 第三个为实际的最后RSI6的值。

Source code in omicron/talib/morph.py

def rsi_watermarks(
    close: np.array, thresh: Tuple[float, float] = None
) -> Tuple[float, float, float]:
    """给定一段行情数据和用以检测顶和底的阈值，返回该段行情中，谷和峰处RSI均值，最后一个RSI6值。

    其中close的长度一般不小于60，不大于120。返回值中，一个为low_wartermark（谷底处RSI值），
    一个为high_wartermark（高峰处RSI值)，一个为RSI6的最后一个值，用以对比前两个警戒值。

    Args:
        close (np.array): 具有时间序列的收盘价
        thresh (Tuple[float, float]) : None适用所有股票，不必更改，也可自行设置。

    Returns:
        返回数组[low_watermark, high_watermark， rsi[-1]], 第一个为最近两个最低收盘价的RSI均值， 第二个为最近两个最高收盘价的RSI均值。
        若传入收盘价只有一个最值，只返回一个。没有最值，则返回None, 第三个为实际的最后RSI6的值。
    """
    assert len(close) >= 60, "must provide an array with at least 60 length!"

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    if close.dtype != np.float64:
        close = close.astype(np.float64)
    rsi = ta.RSI(close, 6)

    pivots = peak_valley_pivots(close, thresh[0], thresh[1])
    pivots[0], pivots[-1] = 0, 0  # 掐头去尾

    # 峰值RSI>70; 谷处的RSI<30;
    peaks_rsi_index = np.where((rsi > 70) & (pivots == 1))[0]
    valleys_rsi_index = np.where((rsi < 30) & (pivots == -1))[0]

    if len(peaks_rsi_index) == 0:
        high_watermark = None
    elif len(peaks_rsi_index) == 1:
        high_watermark = rsi[peaks_rsi_index[0]]
    else:  # 有两个以上的峰，通过最近的两个峰均值来确定走势
        high_watermark = np.nanmean(rsi[peaks_rsi_index[-2:]])

    if len(valleys_rsi_index) == 0:
        low_watermark = None
    elif len(valleys_rsi_index) == 1:
        low_watermark = rsi[valleys_rsi_index[0]]
    else:  # 有两个以上的峰，通过最近的两个峰来确定走势
        low_watermark = np.nanmean(rsi[valleys_rsi_index[-2:]])

    return low_watermark, high_watermark, rsi[-1]

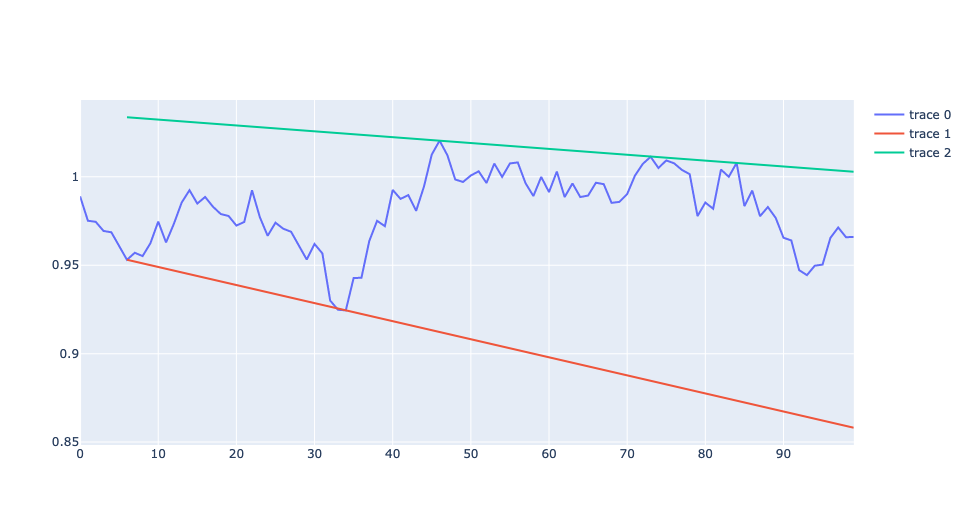
`support_resist_lines(ts, upthres=None, downthres=None)` ¶

计算时间序列的支撑线和阻力线

使用最近的两个高点连接成阴力线，两个低点连接成支撑线。

Examples:

    def show_support_resist_lines(ts):
        import plotly.graph_objects as go

        fig = go.Figure()

        support, resist, x_start = support_resist_lines(ts, 0.03, -0.03)
        fig.add_trace(go.Scatter(x=np.arange(len(ts)), y=ts))

        x = np.arange(len(ts))[x_start:]
        fig.add_trace(go.Line(x=x, y = support(x)))
        fig.add_trace(go.Line(x=x, y = resist(x)))

        fig.show()

    np.random.seed(1978)
    X = np.cumprod(1 + np.random.randn(100) * 0.01)
    show_support_resist_lines(X)

the above code will show this

Parameters:

Name	Type	Description	Default
`ts`	`np.ndarray`	时间序列	required
`upthres`	`float`	请参考peaks_and_valleys	`None`
`downthres`	`float`	请参考peaks_and_valleys	`None`

Returns:

Type	Description
`Tuple[Callable, Callable, numpy.ndarray]`	返回支撑线和阻力线的计算函数及起始点坐标，如果没有支撑线或阻力线，则返回None

Source code in omicron/talib/morph.py

def support_resist_lines(
    ts: np.ndarray, upthres: float = None, downthres: float = None
) -> Tuple[Callable, Callable, np.ndarray]:
    """计算时间序列的支撑线和阻力线

    使用最近的两个高点连接成阴力线，两个低点连接成支撑线。

    Examples:
        ```python
            def show_support_resist_lines(ts):
                import plotly.graph_objects as go

                fig = go.Figure()

                support, resist, x_start = support_resist_lines(ts, 0.03, -0.03)
                fig.add_trace(go.Scatter(x=np.arange(len(ts)), y=ts))

                x = np.arange(len(ts))[x_start:]
                fig.add_trace(go.Line(x=x, y = support(x)))
                fig.add_trace(go.Line(x=x, y = resist(x)))

                fig.show()

            np.random.seed(1978)
            X = np.cumprod(1 + np.random.randn(100) * 0.01)
            show_support_resist_lines(X)
        ```
        the above code will show this ![](https://images.jieyu.ai/images/202204/support_resist.png)

    Args:
        ts (np.ndarray): 时间序列
        upthres (float, optional): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]
        downthres (float, optional): 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]

    Returns:
        返回支撑线和阻力线的计算函数及起始点坐标，如果没有支撑线或阻力线，则返回None
    """
    if ts.dtype != np.float64:
        ts = ts.astype(np.float64)

    pivots = peaks_and_valleys(ts, upthres, downthres)
    pivots[0] = 0
    pivots[-1] = 0

    arg_max = np.argwhere(pivots == 1).flatten()
    arg_min = np.argwhere(pivots == -1).flatten()

    resist = None
    support = None

    if len(arg_max) >= 2:
        arg_max = arg_max[-2:]
        y = ts[arg_max]
        coeff = np.polyfit(arg_max, y, deg=1)

        resist = np.poly1d(coeff)

    if len(arg_min) >= 2:
        arg_min = arg_min[-2:]
        y = ts[arg_min]
        coeff = np.polyfit(arg_min, y, deg=1)

        support = np.poly1d(coeff)

    return support, resist, np.min([*arg_min, *arg_max])

`valley_detect(close, thresh=(0.05, -0.02))` ¶

给定一段行情数据和用以检测近期已发生反转的最低点，返回该段行情中，最低点到最后一个数据的距离和收益率数组，如果给定行情中未找到满足参数的最低点，则返回两个空值数组。

其中bars的长度一般不小于60，不大于120。此函数采用了zigzag中的谷峰检测方法，其中参数默认(0.05,-0.02), 此参数对所有股票数据都适用。若满足参数，返回值中，距离为大于0的整数，收益率是0~1的小数。

Parameters:

Name	Type	Description	Default
`close`	`np.ndarray`	具有时间序列的收盘价	required
`thresh`	`Tuple[float, float])`	请参考peaks_and_valleys	`(0.05, -0.02)`

Returns:

Type	Description
`int`	返回该段行情中，最低点到最后一个数据的距离和收益率数组，如果给定行情中未找到满足参数的最低点，则返回两个空值数组。

Source code in omicron/talib/morph.py

def valley_detect(
    close: np.ndarray, thresh: Tuple[float, float] = (0.05, -0.02)
) -> int:
    """给定一段行情数据和用以检测近期已发生反转的最低点，返回该段行情中，最低点到最后一个数据的距离和收益率数组，
    如果给定行情中未找到满足参数的最低点，则返回两个空值数组。

    其中bars的长度一般不小于60，不大于120。此函数采用了zigzag中的谷峰检测方法，其中参数默认(0.05,-0.02),
    此参数对所有股票数据都适用。若满足参数，返回值中，距离为大于0的整数，收益率是0~1的小数。

    Args:
        close (np.ndarray): 具有时间序列的收盘价
        thresh (Tuple[float, float]) : 请参考[peaks_and_valleys][omicron.talib.morph.peaks_and_valleys]

    Returns:
        返回该段行情中，最低点到最后一个数据的距离和收益率数组，
        如果给定行情中未找到满足参数的最低点，则返回两个空值数组。
    """

    assert len(close) >= 60, "must provide an array with at least 60 length!"

    if close.dtype != np.float64:
        close = close.astype(np.float64)

    if thresh is None:
        std = np.std(close[-59:] / close[-60:-1] - 1)
        thresh = (2 * std, -2 * std)

    pivots = peak_valley_pivots(close, thresh[0], thresh[1])
    flags = pivots[pivots != 0]
    increased = None
    lowest_distance = None
    if (flags[-2] == -1) and (flags[-1] == 1):
        length = len(pivots)
        valley_index = np.where(pivots == -1)[0]
        increased = (close[-1] - close[valley_index[-1]]) / close[valley_index[-1]]
        lowest_distance = int(length - 1 - valley_index[-1])

    return lowest_distance, increased

`vcross(f, g)` ¶

判断序列f是否与g存在类型v型的相交。即存在两个交点，第一个交点为向下相交，第二个交点为向上相交。一般反映为洗盘拉升的特征。

Examples:

>>> f = np.array([ 3 * i ** 2 - 20 * i +  2 for i in range(10)])
>>> g = np.array([ i - 5 for i in range(10)])
>>> flag, indices = vcross(f, g)
>>> assert flag is True
>>> assert indices[0] == 0
>>> assert indices[1] == 6

Parameters:

Name	Type	Description	Default
`f`	`<built-in function array>`	first sequence	required
`g`	`<built-in function array>`	the second sequence	required

Returns:

Type	Description
`Tuple`	(flag, indices), 其中flag取值为True时，存在vcross，indices为交点的索引。

Source code in omicron/talib/morph.py

def vcross(f: np.array, g: np.array) -> Tuple:
    """判断序列f是否与g存在类型v型的相交。即存在两个交点，第一个交点为向下相交，第二个交点为向上
    相交。一般反映为洗盘拉升的特征。

    Examples:

        >>> f = np.array([ 3 * i ** 2 - 20 * i +  2 for i in range(10)])
        >>> g = np.array([ i - 5 for i in range(10)])
        >>> flag, indices = vcross(f, g)
        >>> assert flag is True
        >>> assert indices[0] == 0
        >>> assert indices[1] == 6

    Args:
        f: first sequence
        g: the second sequence

    Returns:
        (flag, indices), 其中flag取值为True时，存在vcross，indices为交点的索引。
    """
    indices = np.argwhere(np.diff(np.sign(f - g))).flatten()
    if len(indices) == 2:
        idx0, idx1 = indices
        if f[idx0] > g[idx0] and f[idx1] < g[idx1]:
            return True, (idx0, idx1)

    return False, (None, None)

core ¶

angle(ts, threshold=0.01, loss_func='re') ¶

clustering(numbers, n) ¶

exp_moving_average(values, window) ¶

mean_absolute_error(y, y_hat) ¶

moving_average(ts, win, padding=True) ¶

normalize(X, scaler='maxabs') ¶

pct_error(y, y_hat) ¶

polyfit(ts, deg=2, loss_func='re') ¶

slope(ts, loss_func='re') ¶

smooth(ts, win, poly_order=1, mode='interp') ¶

weighted_moving_average(ts, win) ¶

morph ¶

BreakoutFlag (IntEnum) ¶

CrossFlag (IntEnum) ¶

breakout(ts, upthres=0.01, downthres=-0.01, confirm=1) ¶

cross(f, g) ¶

energy_hump(bars, thresh=2) ¶

inverse_vcross(f, g) ¶

peaks_and_valleys(ts, up_thresh=None, down_thresh=None) ¶

plateaus(numbers, min_size, fall_in_range_ratio=0.97) ¶

rsi_bottom_distance(close, thresh=None) ¶

rsi_bottom_divergent(close, thresh=None, rsi_limit=30) ¶

rsi_predict_price(close, thresh=None) ¶

rsi_top_distance(close, thresh=None) ¶

rsi_top_divergent(close, thresh=None, rsi_limit=70) ¶

rsi_watermarks(close, thresh=None) ¶

support_resist_lines(ts, upthres=None, downthres=None) ¶

valley_detect(close, thresh=(0.05, -0.02)) ¶

vcross(f, g) ¶

`core` ¶

`angle(ts, threshold=0.01, loss_func='re')` ¶

`clustering(numbers, n)` ¶

`exp_moving_average(values, window)` ¶

`mean_absolute_error(y, y_hat)` ¶

`moving_average(ts, win, padding=True)` ¶

`normalize(X, scaler='maxabs')` ¶

`pct_error(y, y_hat)` ¶

`polyfit(ts, deg=2, loss_func='re')` ¶

`slope(ts, loss_func='re')` ¶

`smooth(ts, win, poly_order=1, mode='interp')` ¶

`weighted_moving_average(ts, win)` ¶

`morph` ¶

`BreakoutFlag (IntEnum)` ¶

`CrossFlag (IntEnum)` ¶

`breakout(ts, upthres=0.01, downthres=-0.01, confirm=1)` ¶

`cross(f, g)` ¶

`energy_hump(bars, thresh=2)` ¶

`inverse_vcross(f, g)` ¶

`peaks_and_valleys(ts, up_thresh=None, down_thresh=None)` ¶

`plateaus(numbers, min_size, fall_in_range_ratio=0.97)` ¶

`rsi_bottom_distance(close, thresh=None)` ¶

`rsi_bottom_divergent(close, thresh=None, rsi_limit=30)` ¶

`rsi_predict_price(close, thresh=None)` ¶

`rsi_top_distance(close, thresh=None)` ¶

`rsi_top_divergent(close, thresh=None, rsi_limit=70)` ¶

`rsi_watermarks(close, thresh=None)` ¶

`support_resist_lines(ts, upthres=None, downthres=None)` ¶

`valley_detect(close, thresh=(0.05, -0.02))` ¶

`vcross(f, g)` ¶